CUWB Probability-on-Sea 8th January 2024
| Minicourse speaker | Title and Abstract |
| Emma Horton (Warwick) | TBA |
| Pierre Francois Rodriguez (Imperial) |
Percolation and random walks Abstract: we will give the flavor of a research area motivated on the one hand by problems arising in statistical physics concerning (continuous) phase transitions, and by fragmentation and covering problems for random walks on the other. The wealth of the subject is notably due to the panoply of natural probabilistic objects that these questions bring into play, comprising for instance random walks, random interlacements and the Gaussian free field, which form a marvellous toolbox to tackle them. The course will be a gentle introduction into some of these ideas. |
| Geronimo Uribe Bravo (UNAM) | TBA |
Talks by:
Osvaldo Angtuncio (UMAR)
Giuseppe Cannizaro (University of Warwick)
Guillaume Conchon-Kerjan (King's College London)
James Foster (University of Bath)
Adrian Gonzalez-Casanova (UNAM)
Karen Harbermann (University of Warwick)
Arturo Jaramillo (CIMAT)
Marcel Ortgiese (University of Bath)
Liliana Perralta (UNAM)
Tommaso Rosati (University of Warwick)
Daniel Valesin (University of Warwick)
Organizers
Daniel Kious, Andreas Kyprianou Giuseppe Cannizaro, Arno Siri-Jégousse, Sandra Palau, Juan Carlos Pardo
Tentative Schedule
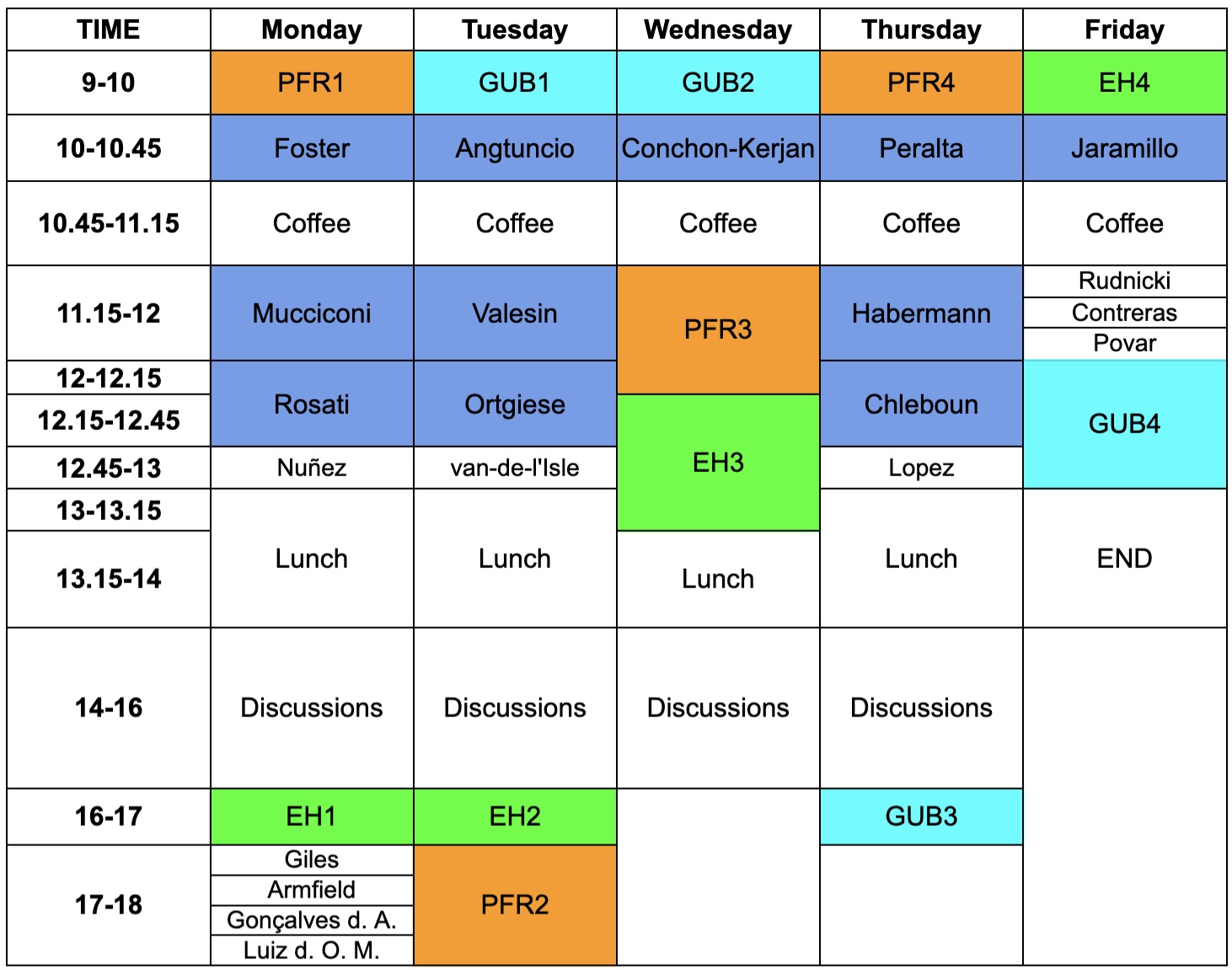
PFR: Mini course by Pierre-François Rodriguez
EH: Mini course by Emma Horton
GUB: Mini course by Geronimo Uribe Bravo